November 2013 Logic & Maths Puzzles
The drawing above represents two shapes made from joining coloured hexagonal tiles together. How many different ways can you place the small shape over the larger shape so that it lines up, making a match with the existing colours?
You can spin the small shape around, but you can’t flip it over.
2. A party of people went to a restaurant and each ordered exactly the same meal. The total bill came to $44.11. How many were in the party? (Clue: not more than 20)
3. Simple Simon met a pieman going to the fair
Said Simple Simon to the pieman, “How much is your ware”?
Said the pieman to Simple Simon, “It’s seven pence for each of these, and eight pence for each of those”.
“Fair enough”, said Simple Simon, and bought some of these and some of those. The whole lot cost 8 shillings and 1 pence.
How many of these and how many of those did he buy?
4. What is the smallest number that increases by 12 when viewed upside down?
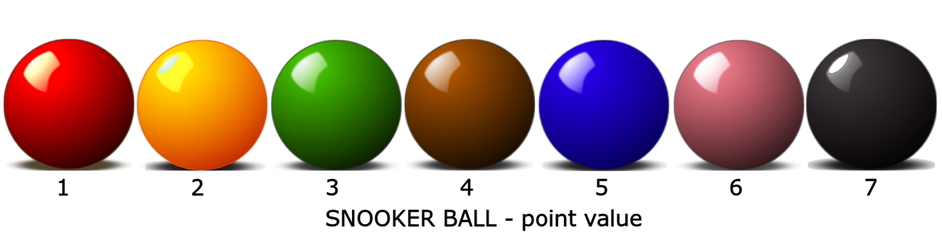
5. A snooker break is made by potting red balls, which are each followed by
a ball of a different colour.
A snooker player makes a break of 70, which finishes when he fails to pot the next red. In the break he pots the same number of blue and brown and one more pink than yellow. None of the other colours is potted.
a) How many red balls were potted in the break?
b) How many yellow?
c) How many brown?
d) How many blue?
e) How many pink?
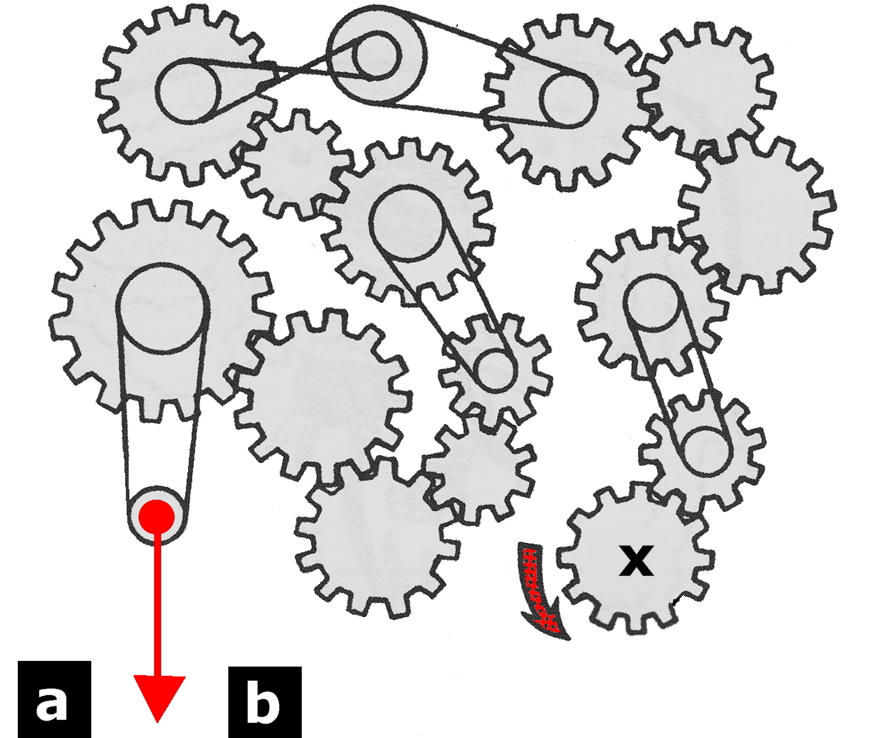
When gear x moves in this train of gears and pulleys rotates in the direction shown, will the red needle make contact with a or b ?
7. Three quarters of the time already passed on a 99 year lease is equal to three fifths of the time left to serve on the lease. How many years have passed on the lease?
8. A small number of cards has been lost from a complete pack.
If I deal to four people, three cards are left over.
If I deal to three people, two cards are left over.
If I deal to five people, two cards are left over.
How many cards are in the incomplete pack?
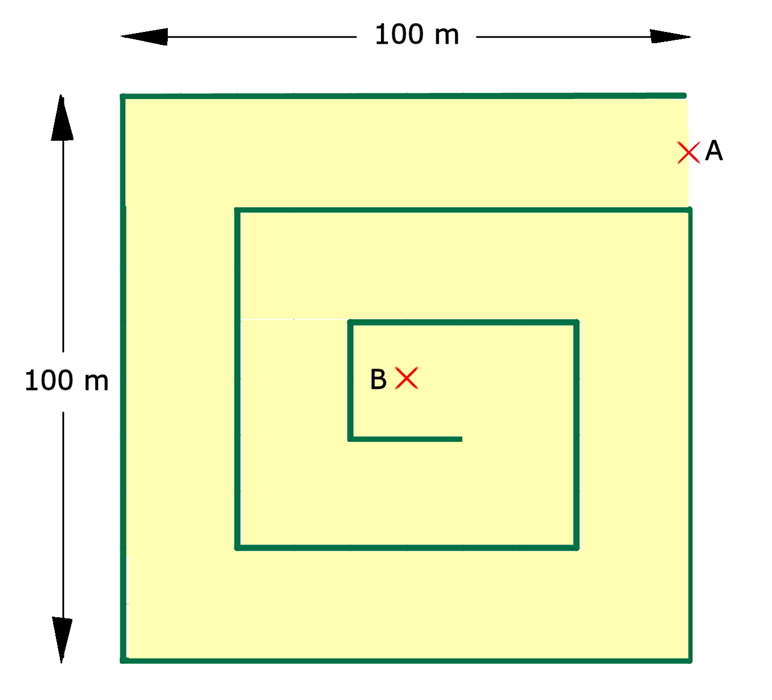
9. The diagram below represents a feature in a park.
A sandy path (yellow) is lined with a narrow hedge.
Ignoring the width of the hedges, the path is an even 20m wide.
If point A is the entrance and point B is the centre of the feature, how far will you have to walk from point A to Point B if you stick to the centre of the path?
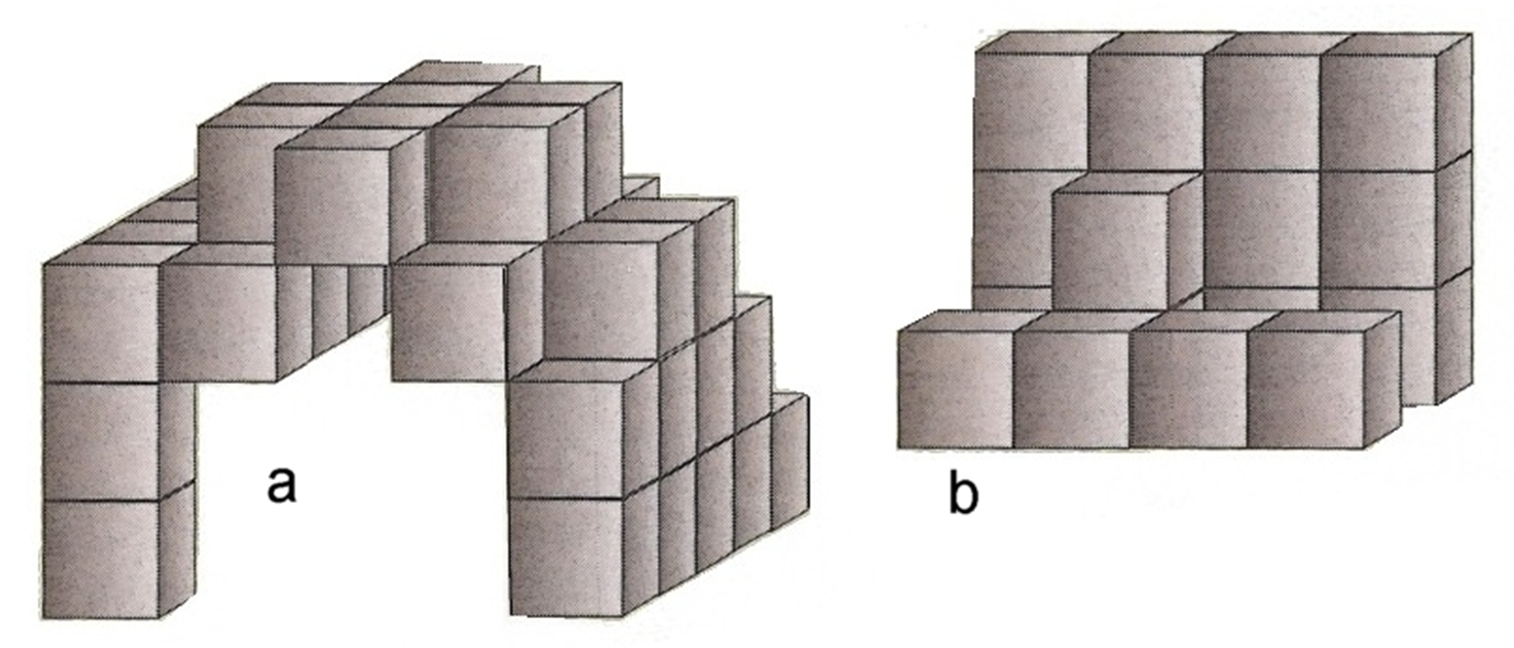
10. In the two designs below, combinations of cubes are stacked together.
All the rows are complete unless you can see their end. In other words, you can assume that there are some unseen cubes behind the visible ones.
Based on the visual evidence given, state how many cubes are in each design.